NÚMEROS COMPLEJOS. Forma polar o trigonométrica.

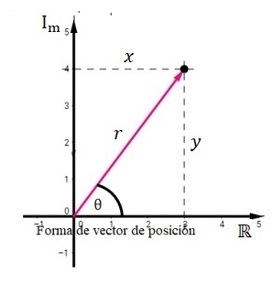
Ahora retorne a la representación de un número complejo en su forma de vector de posición como muestra la figura de la izquierda, de la trigonometría se sabe que: $$\sin{\theta}=\frac{y}{r};\ \ \cos{\theta}=\frac{x}{r};\ \ \tan{\theta}=\frac{y}{x}$$ Despejando \(x\) y \(y\) de estas expresiones se tiene \(x=r\cos{\theta};~~~~~~\ y=r\sin{\theta}\) las cuales son expresiones conocidas como componentes rectangulares de un vector, de donde \(z=x+iy\) puede escribirse en función de sus componentes como \(z=r\cos{\theta}+ir\sin{\theta}\) factorizando \(r\) en la expresión para simplificarla se tiene: $$z=r(\cos{\theta}+i\sin{\theta})~~~~ \mathrm{Forma~polar~o~ trigonométrica~de}~z$$

En cursos posteriores de análisis complejo, mediante el uso de series infinitas se probará que, $$re^{i\theta}=r(\cos{\theta}+i\sin{\theta})$$ la cual es conocida como la identidad de Euler en honor a Leonard Euler y es una manera alternativa para escribir de manera más compacta la forma polar, el número \(r\) es el módulo de \(z\Longrightarrow r=\left|z\right|=\sqrt{x^2+y^2}\).

Además, note que el ángulo theta \(\theta\) no es único, cualquier ángulo phi \(\phi=\theta+2n\pi\) donde \(n\in\mathbb{N}\) cumple las condiciones, $$\sin{\phi}=\frac{y}{r};~~~~\cos{\phi}=\frac{x}{r},$$ Así al referirse al ángulo theta \(\theta\) para diferenciarlo de cualquier otro ángulo phi\(\phi\) que sea coterminal con él, se dice que \(\theta\) es el argumento principal de \(z.\) Por lo general \(\theta\) se mide en radianes y aunque, $$\tan{\theta}=\left(\frac{y}{x}\right)$$ no necesariamente \(\theta\) es la tangente inversa o arco tangente (ángulo cuya tangente tiene el valor \(x/y\), lo cual se escribe como $$\theta=\tan^{-1}{\left(\frac{y}{x}\right)}.$$ Para determinar el argumento principal del complejo \(z=\left(x,y\right)\), los signos de \(y\) y \(x\) proporcionan el cuadrante al cual pertenece \(\theta.\) y se tiene,
\begin{align} \mathrm{Si}&~ (x,y)~\mathrm{se~ ubica~ en~ el~primer~ cuadrante}~~ \theta=\tan^{-1}{\left(\frac{y}{x}\right)}\\ \mathrm{Si}&~(x,y)~\mathrm{se~ ubica~ en~el~segundo~ cuadrante}~~ \theta=\pi+\tan^{-1}\left(\frac{y}{x}\right)\\ \mathrm{Si}&~(x,y) \mathrm{~se ~ubica~ en~el~ tercer~ cuadrante}~~ \theta=\pi+\tan^{-1}{\left(\frac{y}{x}\right)}\\ \mathrm{Si}&~(x,y)~\mathrm{se ~ubica~ en~ el~cuarto~ cuadrante}~~ \theta=2\pi+\tan^{-1}{\left(\frac{y}{x}\right)}\end{align} Recuerde que si se mide en grados \(\pi=180°\)

Ejemplo 1. Determinar la forma polar o trigonométrica de los complejos dados y representarlos en el plano complejo.
\(a)\ 1-i\ \ \ \ \ \ \ b)-\sqrt3+\sqrt3i\ \ \ \ \ \ \ \ c)\ -3-\sqrt3i\ \ \ \ \ \ \ \ \ \ d)\ 2+2i\)
Solución: la forma polar es \(z=re^{i\theta}=r\left(\cos{\theta+i\sin{\theta}}\right)\) por tanto, se debe conocer el módulo \(r\) y argumento principal (ángulo) \(\theta\) de \(z\) observando los signos de \(z=(x,y)\) para cococer el cuadrante donde este se ubica.
Para \(z=1-i\): \(z\) está en el cuarto cuadrante así que, $$\theta=2\pi+\tan^{-1}{\left(\frac{y}{x}\right)}\Longrightarrow\tan^{-1}{\left(-1\right)}=\frac{7\pi}{4}=-\frac{\pi}{4}$$ $$\left\{\begin{array}1r=\sqrt{1^2+1^2}=\sqrt2\\\theta=-\frac{\pi}{4}~~~~~~~~~~~~~~~~~~~~\end{array}\right.\Longrightarrow 2e^{i\frac{π}4}=\sqrt2\left(\cos{\frac{π}{4}}+i\sin\frac{π}{4}\right) $$ Parte b para \(z=-\sqrt3+\sqrt3i\): \(z\) está en el segundo cuadrante, $$\theta=\pi+\tan^{-1}{\left(\frac{y}{x}\right)}=\pi+\tan^{-1}{\left(-1\right)}=\frac{3\pi}{4}$$ $$\left\{\begin{array}1r=\sqrt{(-\sqrt3)^2+(\sqrt3)^2}=\sqrt6\\\theta=\frac{3\pi}{4}~~~~~~~~~~~~~~~~~~~~\end{array}\right.\Longrightarrow \sqrt6e^{i\frac{3π}4}=\sqrt6\left(\cos{\frac{3π}{4}}+i\sin\frac{3π}{4}\right) $$ Note la gran diferencia entre la parte \(a\) y la parte \(b\), en ambos casos se ha determinado \(\tan^{-1}{\left(-1\right)}\), sin embargo, el resultado es muy diferente.

Parte \(c\): \(z=-3-\sqrt3i\) está en el tercer cuadrante, por tanto, $$\theta=\pi+\tan^{-1}{\left(\frac{y}{x}\right)}\Longrightarrow\pi+\tan^{-1}{\left(\frac{\sqrt3}{3}\right)}=\frac{7\pi}{6}$$ $$\left\{\begin{array}1r=\sqrt{\left(3\right)^2+\left(\sqrt3\right)^2}=2\sqrt3\\ \theta=\frac{7\pi}{6}\end{array}\right.\Longrightarrow z=2\sqrt3e^{\frac{7\pi}{6}i}~ó~z=2\sqrt3\left(\cos\frac{7π}{6}+i\sin\frac{7π}{6}\right)$$ Parte \(d\): para \(z=2+2i\) está en el primer cuadrante por lo que, $$\theta=\tan^{-1}{\left(1\right)}\Longrightarrow\theta=\frac{\pi}{4}$$ $$\left\{\begin{array}1r=\sqrt{2^2+2^2}=2\sqrt2\\\theta=\frac{\pi}{4}\end{array}\right.\Longrightarrow z=2\sqrt2e^{i\frac{\pi}4}=2\sqrt2\left(\cos\frac{\pi}4+i\sin\frac{\pi}4\right)$$ Desde luego que se puede utilizar grados al trabajar en la forma polar, basta con recordar que \(\pi ~rad=180°\) y realizar la conversión.

Ejemplo 2. Trabajando con grados Escribir en forma polar el complejo \(\sqrt2-\sqrt2i.\)
Solución: \(z\) se ubica en el cuarto cuadrante, por tanto: $$\theta=2\pi+\tan^{-1}{\left(\frac{y}{x}\right)}\Longrightarrow\theta=2(180°)+\tan^{-1}\left(\frac{\sqrt2}{\sqrt2}\right)=315°$$ $$\left\{\begin{array}1r=\sqrt{(\sqrt2)^2+(\sqrt2)^2}=2\\\theta=315°\end{array} \right.⟹z=2(\cos315°+i\sin315°)$$

Productos y cocientes en forma polar.

Una de las ventajas que tiene la forma polar o trigonométrica de un número complejo es la determinación de productos, cocientes y potencias, mediante una forma sencilla en comparación con los procedimientos algebraicos, como se muestra a continuación.

Sean \(z_1=re^{i\theta}\) y \(z_2=\rho e^{i\varphi}\) dos números complejos cualquieras (distintos de \(z=0\)), los cuales están escritos en su forma polar, entonces es fácil ver por propiedades de los exponentes que:
1. El producto de complejos \(z_1z_2\) está dado por: $$z_1z_2=r\rho e^{i\left(\theta+\varphi\right)}=\left(\cos{\left(\theta+\varphi\right)}+i\sin{\left(\theta+\varphi\right)}\right)$$ 2. El cociente de complejos \(z_1 / z_2\) está dado por: $$\frac{z_1}{z_2}=\frac{r}{\rho}e^{i\left(\theta-\varphi\right)}=\frac{r}{\rho}\left(\cos{\left(\theta-\varphi\right)}+i\sin{\left(\theta-\varphi\right)}\right)$$

Ejemplo 3. Dados los complejos \(z_1=3e^{i\pi}\) y \(z_2=5e^{i\frac{\pi}{3}}\) determinar:
1.El producto \(z_1z_2\)
2.Los cocientes \(z_1 \div z_2\) y \(z_2 \div z_1\)
3.Escribir los resultados en función de senos y cosenos.
4.Escribir los resultados en forma binómica.
Solución 1. $$z_1\left(z_2\right)=3(5)e^{i\pi+i\frac{\pi}{3}}=15e^{i4\frac{\pi}{3}}$$ Solución 2. $$\frac{z_1}{z_2}=\frac{3}{5}e^{i\pi-i\frac{\pi}{3}}=\frac{3}{5}e^{i2\frac{\pi}{3}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{z_2}{z_1}=\frac{5}{3}e^{i\frac{\pi}{3}-i\pi}=\frac{5}{3}e^{-i2\frac{\pi}{3}}$$ Soluciones 3 y 4: \begin{align} z_1z_2&=15\left(\cos{\frac{4\pi}{3}}+i\sin{\frac{4\pi}{3}}\right)=15\left(-\frac{1}{2}+i\frac{\sqrt3}{2}\right)=-\frac{15}{2}+i\frac{15\sqrt3}{2}\\ \frac{z_1}{z_2}&=\frac{3}{5}\left(\cos{\frac{2\pi}{3}}+i\sin{\frac{2\pi}{3}}\right)=\frac{3}{5}\left(-\frac{1}{2}+i\frac{\sqrt3}{2}\right)=-\frac{3}{10}+i\frac{3\sqrt3}{10}\\ \frac{z_2}{z_1}&=\frac{5}{3}\left(\cos{\left(-\frac{2\pi}{3}\right)}+i\sin{\left(-\frac{2\pi}{3}\right)}\right)=\frac{5}{3}\left(\cos{\frac{2\pi}{3}}-i\sin{\frac{2\pi}{3}}\right)\\ \frac{z_2}{z_1}&=\frac{5}{3}\left(-\frac{1}{2}-i\frac{\sqrt3}{2}\right)=-\frac{5}{6}-i\frac{5\sqrt3}{6}\end{align}

Para reforzar su aprendizaje vea los ejercicios resueltos que se plantean en el apartado de ejercicios de la pestaña de arrriba, o dirija su atención hacia otro rumbo, observando las potencias de un número complejo en su forma polar o trigonoétrica, haciendo clic en la pestaña de arriba marcada como Teorema de DeMoivre.

Para más contenidos Ir arriba y luego clic en la pestaña del contenido deseado.

Potencias de un número complejo en forma polar.

Sea \(z=re^{i\theta}=r\left(\cos{\theta+i\sin{\theta}}\right)\) entonces: \begin{array}1 z^2=\left(re^{i\theta}\right)^2=r^2e^{2i\theta}~~~~~~~~&z^3=\left(re^{i\theta}\right)^3=r^3e^{3i\theta}\\ z^4=\left(re^{i\theta}\right)^4=r^4e^{4i\theta}~~~~~~~~&z^n=\left(re^{i\theta}\right)^n=r^ne^{ni\theta}\\ \end{array} que escrita en función de senos y cosenos es, $$\textcolor{navy}{z^n=r^n\left(\cos{n\theta}+i\sin{n\theta}\right)}$$ resultado que es conocido como el teorema de DeMoivre y permite escribir de manera simple las potencias de un complejo. $$\begin{array}{l} {\rm Teorema~ de~ DeMoivre}\\ \hline \mathrm{Si}~ z=r(\cos{\theta}+i\sin{\theta})~~\mathrm{entonces,}\\ z^n=r^n(\cos{n\theta}+i\sin{n\theta})\\ \end{array}$$ El uso de este teorema se presenta en los siguientes ejemplos como sigue.

Ejemplo 1. Determinar \(z^2\) y \(z^4\) dado \(z=2+2i\).
Solución: si se desarrolla \(\left(2+2i\right)^2=8i\) se puede escribir la solución como \((2+2i)^2=8i=(0,8)\). sin la usar el terema de DeMoivre
Para \(z^4\) se puede proceder al igual que para \(z^2\) si conoce el desarrollo de Newton de esta potencia, mediante el uso del teorema de DeMoivre el resultado es como sigue. $$z^4=r^4(\cos{4\theta}+i\sin{4\theta})$$ Donde el módulo \(r=\sqrt{2^2+2^2}=2\sqrt2\) y para el argumento principal \(\theta\) se observa que el complejo \(z=2+2i\) se ubica en el primer cuadrante por tanto, $$\theta=\tan^{-1}\left(\frac{2}{2}\right)=\frac{\pi}{4}$$ de donde \(z^4=64\left(\cos{\pi}+i\sin{\pi}\right)\) que es la solución buscada.
En caso se que se pidan otras representaciones para este complejo, la forma exponencial es \(z^4=64e^{i\pi}\), la forma de par odrdenado \((-64,0)\) y la forma binómica \(z^4=-64+0i\) donde es innecesario el \(0i\).

Ejemplo 2. Dado \(z=-3-\sqrt3i\) determinar \(z^{10}\).
Solución: comience por determinar el módulo \(r=\sqrt{(-3)^2+(-3)^2}=2\sqrt3\) y el argumento principal theta, ubicado en el tercer cuadrante. $$\theta=\pi + \tan^{-1}\frac{-\sqrt3}{-3}=\frac{7\pi}{6}$$ por tanto, $$z^{10}=(2\sqrt3)^{10}e^{i\frac{70}{6}}=(2\sqrt3)^{10}e^{i\frac{35}{3}}$$ que en términos de seno y coseno es, $$z^{10}=\left(2\sqrt3\right)^{10}\left(\cos{\frac{35\pi}{3}}+i\ \sin{\frac{35\pi}{3}}\right)$$

Para más contenidos Ir arriba y luego clic en la pestaña del contenido deseado.